Intro to Phase-encoding - I
I understand frequency-encoding, but I just don't get phase-encoding. Can you explain?
|
|
You are not alone. Phase-encoding is at first a somewhat difficult concept to get one's head around. Let me try to approach this in a couple of different ways.
|
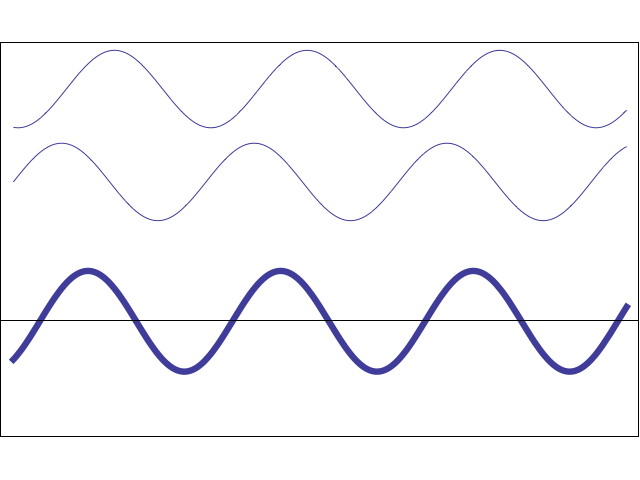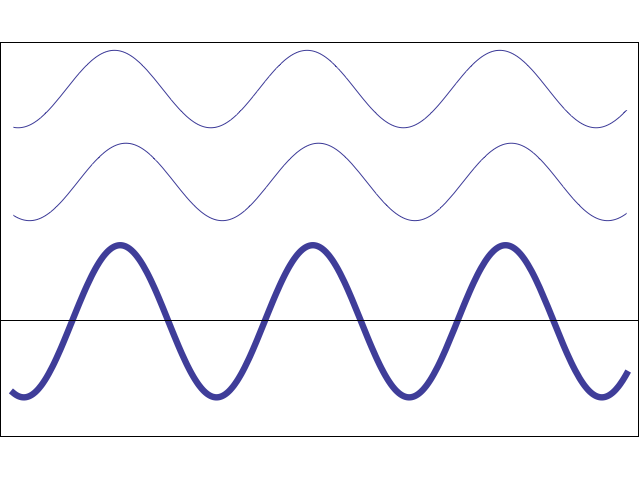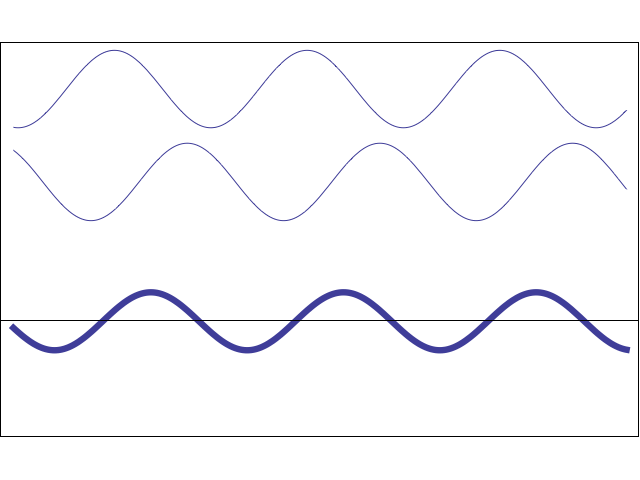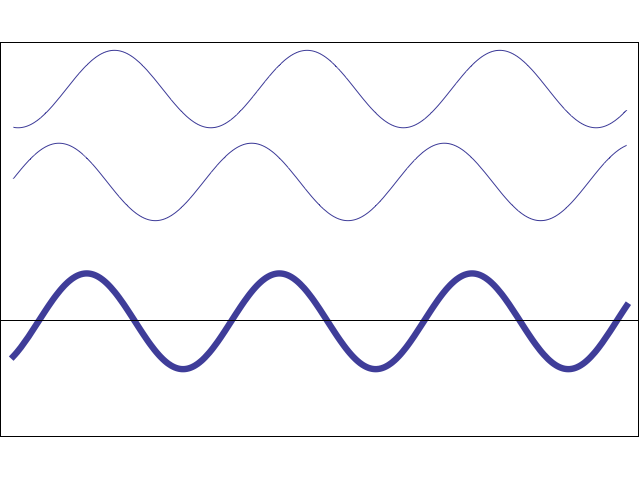
Recall that when two sine waves (A and B) with the same frequency but different phases are added together, the result is another sine wave with the same frequency but a different phase. When the sine waves are close together in phase they constructively interfere, and when out of phase they destructively interfere.
The important point is this: Looking only at their sum, you simply see a sine wave of a certain frequency and phase. It is impossible from this single observation to sort out the individual contributions made by waves A and B. |
Interference of two sine waves of same frequency but different phases. (Courtesy of Dr. Dan Russell, Grad. Prog. Acoustics, Penn State)
|
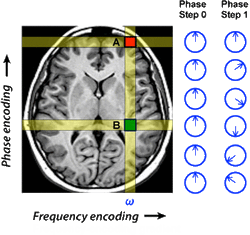
However, by making two observations with A and B shifted by different phases, it is possible to determine their individual contributions by looking only at their sums. This is illustrated below in an MR image, where A and B are two pixels in the same vertical column resonating at the same encoded frequency (ω). Specifically, at Step 0 (baseline, when no phase-encoding gradient is has been applied) the total signal from A&B together can be written: So(t) = A sin ωt + B sin ωt = (A+B) sin ωt.
|
|
|
In Step 1 we apply a phase encoding gradient to dephase spins along the vertical axis. After the gradient has been turned off, the signal from each pixel in the AB column now has a different phase shift, represented by the small clock face arrows.
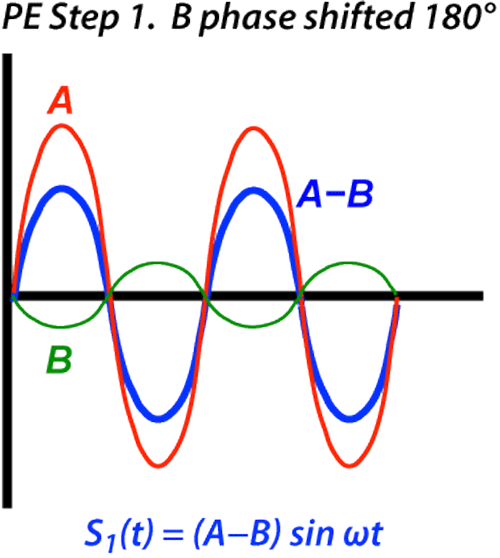
Let us ignore all the other pixels and just concentrate on A and B. Furthermore, for simplicity, let us assume that pixel A was in the zero position of the phase-encoding gradient and did not change phase, while pixel B was in a higher portion of the gradient and gained exactly 180° of phase relative to A.
The signal emitted from pixel A is unchanged and equals A sin ωt. The signal from pixel B is now inverted and equals −B sin ωt. The total signal from A&B is now S1(t) = A sin ωt − B sin ωt = (A−B) sin ωt.
The signal emitted from pixel A is unchanged and equals A sin ωt. The signal from pixel B is now inverted and equals −B sin ωt. The total signal from A&B is now S1(t) = A sin ωt − B sin ωt = (A−B) sin ωt.
From this single measurement in Step 1, we still do not know the individual amplitudes A and B, only their difference (A−B). Using information from both Step 0 and Step 1 together, we are able to extract the unique signal contributions by simple algebra:
½ [So + S1] = ½ [(A+B) + (A−B)] = A and ½ [So − S1] = ½ [(A+B) − (A−B)] = B
References
Edelstein WA, Hutchison JMS, Johnson G, Redpath TW. Spin warp NMR imaging and application to human whole-body imaging. Phys Med Biol 1980; 25:751-756. (The spin-warp method is the classic and dominant method for MR encoding by phase and frequency used for most of the last 35 years.)
Edelstein WA, Hutchison JMS, Johnson G, Redpath TW. Spin warp NMR imaging and application to human whole-body imaging. Phys Med Biol 1980; 25:751-756. (The spin-warp method is the classic and dominant method for MR encoding by phase and frequency used for most of the last 35 years.)
Related Questions
I understand the 2-pixel example, but I still can't put it all together with the whole image and frequency encoding. Can you help?
I understand the 2-pixel example, but I still can't put it all together with the whole image and frequency encoding. Can you help?